Задачи на радиоактивность с решениями
Содержание:
- Оценить уравнения
- 10 6 секунд (мегасекунды)
- Что происходит в организме человека
- Стабильность периода полураспада
- Вероятностный характер
- Ссылки [ править ]
- Один из множества
- Случаи отравления
- Формулы для периода полураспада при экспоненциальном распаде
- Признаки ускоренного радиоактивного распада
- 10 −6 секунд (микросекунды)
- Период полураспада радиоактивного вещества
- Закон радиоактивного распада
- В биологии и фармакологии [ править ]
- Период полураспада
- Многоликий цезий
Оценить уравнения
Устранение первого порядка
Периоды времени применяются к процессам, в которых скорость исключения экспоненциальна. Если C(т){ displaystyle C (t)} это концентрация вещества во времени т{ displaystyle t}, его зависимость от времени определяется выражением
- C(т)=C()е−kт{ Displaystyle С (т) = С (0) е ^ {- kt} ,}
куда k это константа скорости реакции. Такая скорость распада возникает из-за где скорость выведения пропорциональна количеству вещества:
- dCdт=−kC.{ displaystyle { frac {dC} {dt}} = — kC.}
Период полураспада этого процесса составляет
- т12=пер2k.{ displaystyle t _ { frac {1} {2}} = { frac { ln 2} {k}}. ,}
Период полураспада определяется оформление (CL) и объем распространения (VD), и эта связь описывается следующим уравнением:
- т12=пер2⋅VDCL{ displaystyle t _ { frac {1} {2}} = { frac {{ ln 2} cdot {V_ {D}}} {CL}} ,}
В клинической практике это означает, что для достижения стабильного состояния концентрации препарата в сыворотке крови требуется в 4-5 раз больше времени полужизни после начала, остановки или изменения дозы. Так, например, у дигоксина есть период полураспада (или t½) 24–36 ч; это означает, что изменение дозы займет лучшую часть недели, чтобы добиться полного эффекта. По этой причине препараты с длительным периодом полувыведения (например, амиодарон, исключение t½ около 58 дней) обычно начинаются с ударная доза для более быстрого достижения желаемого клинического эффекта.
Двухфазный период полураспада
Для многих препаратов характерна двухфазная кривая выведения — сначала крутой наклон, затем пологий:
- ШАГОВАЯ (начальная) часть кривой -> начальное распределение препарата в организме.
- МАЛЕНЬКАЯ часть кривой -> окончательное выведение лекарственного средства, которое зависит от высвобождения лекарственного средства из отделов ткани в кровь.
Более длительный период полураспада называется конечный период полураспада а период полураспада самого большого компонента называется доминирующий период полураспада. Более подробное описание см. .
10 6 секунд (мегасекунды)
| изотоп | период полураспада | |
|---|---|---|
| дней | 10 6 секунд | |
| фосфор-32 | 14.29 | 1,235 |
| радий-225 | 14,9 | 1,29 |
| висмут-205 | 15.31 | 1,323 |
| ванадий-48 | 15,9735 | 1,38011 |
| протактиний-230 | 17,4 | 1,50 |
| калифорний-253 | 17,81 | 1,539 |
| торий-227 | 18,68 | 1,614 |
| эйнштейний-253 | 20,47 | 1,769 |
| уран-230 | 20,8 | 1,80 |
| торий-234 | 24.10 | 2,082 |
| протактиний-233 | 26,975 | 2,3306 |
| кюрий-240 | 27 | 2.3 |
| хром-51 | 27,7025 | 2,39350 |
| менделевий-260 | 27,8 | 2,40 |
| кюрий-241 | 32,8 | 2,83 |
| эйнштейний-255 | 39,8 | 3,44 |
| плутоний-237 | 45,2 | 3,91 |
| менделевий-258 | 51,5 | 4,45 |
| бериллий-7 | 53,12 | 4,590 |
| калифорний-254 | 60,5 | 5,23 |
| кобальт-56 | 77,27 | 6,676 |
| скандий-46 | 83,79 | 7,239 |
| сера-35 | 87,32 | 7,544 |
| тулий-168 | 93,1 | 8,04 |
| фермий-257 | 100,5 | 8,68 |
| тулий-170 | 128,6 | 11.11 |
| полоний-210 | 138,376 | 11,9557 |
| кальций-45 | 162,7 | 14.06 |
| кюрий-242 | 162,8 | 14.07 |
| золото-195 | 186,1 | 16.08 |
| цинк-65 | 243,7 | 21.06 |
| кобальт-57 | 271,79 | 23 483 |
| эйнштейний-254 | 275,7 | 23,82 |
| ванадий-49 | 330 | 29 |
| берклий-249 | 330 | 29 |
| калифорний-248 | 333,5 | 28,81 |
| годы | 10 6 секунд | |
| рутений-106 | 1.023 | 32,3 |
| нептуний-235 | 1,0845 | 34,22 |
| кадмий-109 | 1,267 | 40,0 |
| эйнштейний-252 | 1,2915 | 40,76 |
| торий-228 | 1,9116 | 60,33 |
| тулий-171 | 1,92 | 61 |
| цезий-134 | 2,0652 | 65,17 |
| натрий-22 | 2,602 | 82,1 |
| калифорний-252 | 2,645 | 83,5 |
| железо-55 | 2,756 | 87,0 |
| плутоний-236 | 2,858 | 90,2 |
| полоний-208 | 2,898 | 0,2504 |
| родий-101 | 3.3 | 100 |
| кобальт-60 | 5,2714 | 166,35 |
| радий-228 | 5,75 | 181 |
| криптон-85 | 10,756 | 339,4 |
| водород-3 (также известный как тритий ) | 12,32 | 389 |
| калифорний-250 | 13.08 | 413 |
| плутоний-241 | 14,290 | 451,0 |
| ниобий-93m | 16,13 | 509 |
| кюрий-244 | 18.10 | 571 |
| актиний-227 | 21,772 | 687,1 |
| свинец-210 | 22,3 | 700 |
| стронций-90 | 28,79 | 909 |
| кюрий-243 | 29,1 | 920 |
| цезий-137 | 30,17 | 952 |
Что происходит в организме человека
Главные пути попадания цезия в организм – через пищеварительный тракт и дыхательные пути. При наружном попадании цезия-137 на неповрежденную кожу проникает внутрь 0,007 %. При попадании внутрь организма 80 % его накапливается в скелетных мышцах.
Выводится элемент через почки и кишечник. В течение месяца выводится до 80 % цезия. В соответствии с данными Международной комиссии по радиологической защите период полувыведения радионуклида составляет семьдесят дней, но скорость зависит от состояния организма, возраста, питания и других факторов.
Радиационные поражения, схожие по симптоматике с лучевой болезнью, развиваются при получении дозы более 2 Гр. Но уже при единицах МБк наблюдаются признаки легкого лучевого поражения в виде диареи, внутренних кровотечений, слабости.
Стабильность периода полураспада
Во всех наблюдавшихся случаях (кроме некоторых изотопов, распадающихся путём электронного захвата) период полураспада был постоянным (отдельные сообщения об изменении периода были вызваны недостаточной точностью эксперимента, в частности, неполной очисткой от высокоактивных изотопов). В связи с этим период полураспада считается неизменным. На этом основании строится определение абсолютного геологического возраста горных пород, а также радиоуглеродный метод определения возраста биологических останков: зная концентрацию радиоизотопа в настоящее время и в прошлом, можно рассчитать, сколько точно времени прошло с тех пор.
Предположение об изменяемости периода полураспада используется креационистами, а также представителями т. н. «альтернативной науки» для опровержения научной датировки горных пород, остатков живых существ и исторических находок, с целью дальнейшего опровержения научных теорий, построенных с использованием такой датировки. (См., например, статьи Креационизм, Научный креационизм, Критика эволюционизма, Туринская плащаница).
Вариабельность постоянной распада для электронного захвата наблюдалась в эксперименте, но она лежит в пределах процента во всём доступном в лаборатории диапазоне давлений и температур. Период полураспада в этом случае изменяется в связи с некоторой (довольно слабой) зависимостью плотности волновой функции орбитальных электронов в окрестности ядра от давления и температуры. Существенные изменения постоянной распада наблюдались также для сильно ионизованных атомов (так, в предельном случае полностью ионизованного ядра электронный захват может происходить только при взаимодействии ядра со свободными электронами плазмы; кроме того, распад, разрешённый для нейтральных атомов, в некоторых случаях для сильно ионизованных атомов может быть запрещён кинематически). Все эти варианты изменения постоянных распада, очевидно, не могут быть привлечены для «опровержения» радиохронологических датировок, поскольку погрешность самого радиохронометрического метода для большинства изотопов-хронометров составляет более процента, а высокоионизованные атомы в природных объектах на Земле не могут существовать сколько-нибудь длительное время.
Поиск возможных вариаций периодов полураспада радиоактивных изотопов, как в настоящее время, так и в течение миллиардов лет, интересен в связи с гипотезой о вариациях значений фундаментальных констант в физике (постоянной тонкой структуры, константы Ферми и т. д.). Однако тщательные измерения пока не принесли результата — в пределах погрешности эксперимента изменения периодов полураспада не были найдены. Так, было показано, что за 4,6 млрд лет константа α-распада самария-147 изменилась не более чем на 0,75 %, а для β-распада рения-187 изменение за это же время не превышает 0,5 %; в обоих случаях результаты совместимы с отсутствием таких изменений вообще.
Вероятностный характер
Моделирование множества идентичных атомов, подвергающихся радиоактивному распаду, начиная с 4 атомов в коробке (слева) или 400 (справа). Число вверху показывает, сколько полураспада прошло
Обратите внимание на следствие закона больших чисел : чем больше атомов, тем общий распад более регулярный и более предсказуемый.
Период полураспада обычно описывает распад дискретных объектов, таких как радиоактивные атомы. В этом случае нельзя использовать определение, которое гласит, что «период полураспада — это время, необходимое для распада ровно половины объектов». Например, если имеется только один радиоактивный атом, а его период полураспада составляет одну секунду, через одну секунду не останется «половины атома».
Вместо этого период полураспада определяется с точки зрения вероятности : «Период полураспада — это время, необходимое для разложения ровно половины сущностей в среднем ». Другими словами, вероятность распада радиоактивного атома в период полураспада составляет 50%.
Например, изображение справа представляет собой симуляцию множества идентичных атомов, подвергающихся радиоактивному распаду
Обратите внимание, что после одного периода полураспада остается не точно половина атомов, только приблизительно , из-за случайного изменения в процессе. Тем не менее, когда распадается много идентичных атомов (правые прямоугольники), закон больших чисел предполагает, что это очень хорошее приближение, чтобы сказать, что половина атомов остается после одного периода полураспада.
Различные простые упражнения могут продемонстрировать вероятностный распад, например, с подбрасыванием монет или запуском статистической компьютерной программы .
Ссылки [ править ]
- Джон Ayto, 20th Century Words (1989), Cambridge University Press.
- Мюллер, Ричард А. (12 апреля 2010 г.). . Издательство Принстонского университета . стр. -129. ISBN .
- ↑ Chivers, Sidney (16 марта 2003 г.). . MADSCI.org.
- . Exploratorium.edu . Проверено 25 апреля 2012 .
- Валлин, Джон (сентябрь 1996). . Astro.GLU.edu. Архивировано 29 сентября 2011 года.
- ^ Рёш, Франк (12 сентября 2014 г.). Ядерная и радиохимия: Введение . 1 . Вальтер де Грюйтер . ISBN 978-3-11-022191-6.
- Джонатан Кроу; Тони Брэдшоу (2014). . п. 568. ISBN
- Lin VW; Карденас Д.Д. (2003). . Демос Медикал Паблишинг, ООО. п. 251. ISBN.
- Пан, Сяо-Фэн (2014). Вода: молекулярная структура и свойства . Нью-Джерси: World Scientific. п. 451. ISBN. .
- Австралийское управление по пестицидам и ветеринарным лекарствам (31 марта 2015 г.). . Правительство Австралии . Проверено 30 апреля 2018 года .
- Фантке, Питер; Гиллеспи, Бренда У .; Джураске, Ронни; Джоллиет, Оливье (11 июля 2014 г.). . Наука об окружающей среде и технологии . 48 (15): 8588–8602. Bibcode . DOI . PMID .
- Balkew, Тешоме Mogessie (декабрь 2010). (тезис). Государственный университет Восточного Теннесси.
- Ирландия, MW, изд. (1928). Медицинский департамент армии США во время мировой войны, т. IX: Инфекционные и другие болезни . Вашингтон: США: Типография правительства США. С. 116–7.
Один из множества
Цезий в периодической таблице Дмитрия Менделеева относится к главной подгруппе первой группы шестого периода и имеет атомный номер 55. Химический символ элемента — Cs (Caesium), и свое название он получил благодаря наличию в спектре относительной интенсивности электромагнитного излучения двух синих линий (от латинского слова caesius, что означает «небесно-голубой»).
Как простое вещество цезий представляет собой мягкий серебристо-желтый металл с выраженными щелочными особенностями.
Открыли этот элемент в 1860 году два ученых из Германии Р. Бунзен и Г. Кирхгоф. Они использовали метод спектрального анализа, и цезий стал первым элементом, который был обнаружен данным способом.

Случаи отравления
Истории известно лишь два таковых. Один произошел в 2006 году – полонием-210 отравили 43-летнего Александра Вальтеровича Литвиненко, подполковника советской и российской госбезопасности, пребывавшего на тот момент в Лондоне.
В ночь на 23 ноября его состояние резко ухудшилось, и меньше чем через сутки он скончался. Тело Александра не вскрывали долгое время, поскольку было опасение облучения медиков радиацией. Были проведены подробнейшие расследования. В их рамках удалось обнаружить следы радиации в тех местах, где был Александр перед тем, как ему стало плохо.
Второй случай не столь однозначный. Полоний-210 был обнаружен в личных вещах председателя Палестинской национальной администрации по имени Ясир Арафат, который умер в 2004 году.
Была даже проведена эксгумация его тела, и швейцарская сторона международной комиссии в результате исследований подтвердила – это отравление изотопом. Но потом все-таки они изменили решение. В итоге российская, французская и швейцарская стороны пришли к тому, что доказательств, подтверждающих факт отравления полония, нет, и дело было закрыто.
Формулы для периода полураспада при экспоненциальном распаде
Экспоненциальный спад можно описать любой из следующих трех эквивалентных формул::109–112
N(т)=N(12)тт12N(т)=Nе−тτN(т)=Nе−λт{displaystyle {egin {align} N (t) & = N_ {0} left ({frac {1} {2}} ight) ^ {frac {t} {t_ {1/2}}}} N (t) & = N_ {0} e ^ {- {frac {t} {au}}} N (t) & = N_ {0} e ^ {- лямбда t} конец {выровнено}}}
куда
- N — начальное количество вещества, которое будет распадаться (это количество может быть измерено в граммах, молях, количестве атомов и т. д.),
- N(т) — это количество, которое все еще остается и еще не разложилось через некоторое время. т,
- т1⁄2 — период полураспада распадающегося количества,
- τ это положительное число называется средняя продолжительность жизни затухающего количества,
- λ положительное число, называемое постоянная распада убывающего количества.
Три параметра т1⁄2, τ, и λ все напрямую связаны следующим образом:
т12=пер(2)λ=τпер(2){displaystyle t_ {1/2} = {frac {ln (2)} {lambda}} = au ln (2)}
где ln (2) — натуральный логарифм 2 (примерно 0,693).:112
Распад двумя или более процессами
Некоторые величины одновременно распадаются за счет двух процессов экспоненциального затухания. В этом случае фактический период полураспада Т1⁄2 может быть связано с периодом полураспада т1 и т2 что количество имело бы, если бы каждый из процессов распада действовал изолированно:
- 1Т12=1т1+1т2{displaystyle {frac {1} {T_ {1/2}}}} = {frac {1} {t_ {1}}} + {frac {1} {t_ {2}}}}
Для трех или более процессов аналогичная формула имеет вид:
- 1Т12=1т1+1т2+1т3+⋯{displaystyle {frac {1} {T_ {1/2}}}} = {frac {1} {t_ {1}}} + {frac {1} {t_ {2}}} + {frac {1} {t_ {3}}} + cdots}
Для доказательства этих формул см. .
Примеры
Период полураспада продемонстрирован с использованием кубиков в классный эксперимент
Существует период полураспада, описывающий любой процесс экспоненциального распада. Например:
- Как отмечалось выше, в радиоактивный распад период полураспада — это промежуток времени, по истечении которого существует 50% -ная вероятность того, что атом подвергнется ядерный разлагаться. Он варьируется в зависимости от типа атома и изотоп, и обычно определяется экспериментально. Видеть Список нуклидов.
- Ток, протекающий через RC схема или же Цепь RL распадается с периодом полураспада ln (2)RC или ln (2)L / R, соответственно. В этом примере термин половина времени имеет тенденцию использоваться, а не «период полураспада», но они означают одно и то же.
- В химическая реакция, период полураспада вида — это время, необходимое для того, чтобы концентрация этого вещества упала до половины от его первоначального значения. В реакции первого порядка период полураспада реагента составляет ln (2) /λ, куда λ это константа скорости реакции.
Признаки ускоренного радиоактивного распада
Если радиоактивный распад длился миллионы, а тем более, миллиарды лет, то диффузия аргона и свинца была недостаточной, в воздухе слишком мало гелия, а в горных породах — слишком много.
Недавние эксперименты группы RATE позволяют сделать вывод, что распад, кажущийся длившимся «полтора миллиона лет», действительно происходил, но на самом деле для него потребовались один или несколько очень коротких периодов времени, имевших место от 4000 до 8000 лет назад. А значит, иллюзия возраста нашей планеты в целом в «4,5 миллиардов лет» тает на глазах и превращается в несколько тысяч лет.
Такой результат получен экстракцией твёрдых, плотных микроскопических кристаллов — цирконов. Бóльшая часть урана и тория в континентальной коре Земли находится в цирконах, часто в виде включений в чешуйках биотита — чёрной слюды. Гелий является продуктом распада урана до свинца. Распад атома урана сопровождается испусканием восьми альфа-частиц — ядер атомов гелия. Каждое из этих ядер быстро захватывает из кристалла по два электрона, и положительный ион становится нейтральным атомом.
Проведённые в Лос-Аламосе измерения количеств урана, тория и свинца показали, что если бы распад происходил с параметрами, наблюдаемыми сейчас, ему бы действительно пришлось занять «полтора миллиарда» лет. Вычислив, сколько гелия накопилось в ходе распада, исследователи затем измерили, сколько его соталось в цирконах. Оказалось, что до 58 % этого элемента не диффундировало из цирконов; процентное соотношение уменьшалось с увеличением глубины и температуры.
В период, когда группа RATE только начинала свою работу, скорости диффузии для цирконов и биотита ещё не были измерены. На основании обнаружения гелия в цирконах доктор ] вычислил скорости диффузии гелия как для креационной, так и для униформистской моделей. Он определил, что отношение между скоростями диффузий для этих моделей составляет примерно сто тысяч раз.
После измерения скоростей диффузии в цирконах оказалось, что с креационной моделью они сопоставимы, а с униформистской — полностью несовместимы. Эти результаты, вместе с фактическим наличием гелия в цирконах, показали, что период, в течение которого шла диффузия, составлял 6000 ± 2000 лет. Этот результат расходится с униформистской моделью в 250000 раз. То есть, на самом деле распад урана никак не мог занять «полтора миллиарда» лет.
Накопить так мало гелия за целых «полтора миллиарда» лет цирконы могли бы лишь в том случае, если бы в течение всего этого периода находились при температуре жидкого азота (-196 градусов Цельсия ниже нуля), что, естественно, противоречит любым предполагаемым сценариям истории Земли.
См. также: Критика данных по распаду гелия, полученных группой RATE
Имеются некоторые свидетельства корреляции между скоростями радиоактивного распада и расстоянием от объекта до Солнца. Джер Дженкинс и др. в Университете Пердью перепроверили необработанные данные различных экспериментов и подтвердили этот вывод.
10 −6 секунд (микросекунды)
| изотоп | Период полураспада 10 -6 секунд |
|---|---|
| свинец-196м2 | <1 |
| полоний-192м | ~ 1 |
| радон-210м3 | 1.04 |
| торий-219 | 1.05 |
| полоний-206м2 | 1.05 |
| радон-210м2 | 1.06 |
| кюрий-243м | 1.08 |
| актиний-218 | 1.08 |
| свинец-192м2 | 1.1 |
| плутоний-237м2 | 1.1 |
| свинец-197м2 | 1,15 |
| америций-241m | 1.2 |
| радий-215м2 | 1,39 |
| висмут-211м | 1.4 |
| уран-222 | 1.4 |
| радий-217 | 1,63 |
| нептуний-223 | 2,15 |
| радий-210м | 2,24 |
| радон-215 | 2.30 |
| висмут-217м | 2,70 |
| полоний-211м3 | 2,8 |
| радон-209м2 | 3.0 |
| висмут-202м1 | 3,04 |
| полоний-213 | 3,65 |
| свинец-198м1 | 4,19 |
| протактиний-221 | 4.9 |
| астатин-210м2 | 5,66 |
| нобелий-250 | 5,7 |
| свинец-212м | 6.0 |
| свинец-214м | 6.2 |
| висмут-187м2 | 7 |
| торий-229м | 7 |
| радий-215м1 | 7.1 |
| свинец-190м3 | 7.2 |
| плутоний-239м2 | 7,5 |
| висмут-206m1 | 7,7 |
| астатин-205м | 7,76 |
| торий-220 | 9,7 |
| свинец-195м2 | 10.0 |
| свинец-199м2 | 10.1 |
| радий-212м1 | 10.9 |
| астатин-196м2 | 11 |
| актиний-219 | 11,8 |
| радон-209м1 | 13,4 |
| полоний-194m | 15 |
| франций-217 | 16,8 |
| уран-223 | 21 год |
| плутоний-241м2 | 21 год |
| фермий-251m | 21,1 |
| кюрий-249m | 23 |
| резерфорд-254 | 23 |
| свинец-205м1 | 24,2 |
| нептуний-220 | 25 |
| свинец-190м2 | 25 |
| радий-218 | 25,2 |
| свинец-189м2 | 26 год |
| кюрий-247m1 | 26,3 |
| берклий-250м1 | 29 |
| нобелий-253m | 31 год |
| полоний-186 | 34 |
| америций-238m | 35 год |
| нобелий-250м | 36 |
| нептуний-224 | 38 |
| калифорний-249m | 45 |
| радон-216 | 45 |
| резерфорд-253 | 48 |
| висмут-185м | 49 |
| полоний-207м2 | 49 |
| радий-231м | ~ 53 |
| уран-219 | 55 |
| берклий-251м | 58 |
| америций-246м2 | 73 |
| сиборгий-261m | 92 |
| астатин-215 | 100 |
| астатин-216м | 100 |
| протактиний-218 | 113 |
| свинец-206м1 | 125 |
| торий-216m1 | 137 |
| кюрий-248m | 146 |
| нептуний-219 | 150 |
| астатин-212м2 | 152 |
| полоний-214 | 164,3 |
| радон-207м | 181 |
| висмут-207м | 182 |
| дармштадтий-270 | 205 |
| берклий-250м2 | 213 |
| дармштадтий-269 | 230 |
| свинец-178 | 230 |
| коперниций-277 | 240 |
| торий-217 | 240 |
| дармштадций-273 | 240 |
| берклий-249м | 300 |
| астатин-216 | 300 |
| висмут-187m1 | 320 |
| нихоний-278 | 340 |
| хасиум-265м | 360 |
| фермий-258 | 370 |
| полоний-188 | 430 |
| актиний-216 | 440 |
| актиний-216m | 443 |
| астатин-210м1 | 482 |
| полоний-187m | 500 |
| хассий-264 | 540 |
| радон-217 | 540 |
| полоний-205м2 | 645 |
| коперниций-277 | 690 |
| Оганессон-294 | 690 |
| фермий-241 | 730 |
| хассий-263 | 760 |
| фермий-242 | 800 |
| висмут-206м2 | 890 |
| менделевий-245 | 900 |
| коперниций-282 | 910 |
| уран-224 | 940 |
Период полураспада радиоактивного вещества
« Период полураспада » или период полураспада радиоактивного изотопа — это время, по истечении которого количество ядер этого изотопа, присутствующих в образце, уменьшается вдвое. Обычно обозначается буквой T или t ½ .
Если мы наблюдаем образец радиоактивного материала, через время t 1/2 , этот образец (по определению) потеряет половину своего материала, и останется только половина исходного материала. Но по истечении этого времени дважды потеря дополнительного материала относится только к оставшейся половине, а не к исходной сумме; после двойного t ½ останется половина половины исходного материала, то есть четверть. Точно так же после трехкратного увеличения t ½ останется только (1/2) 3 = 1/8 первоначальной выборки и так далее. После того, как этот период полураспада будет увеличиваться в десять раз, активность снизится в 2 10 = 1024 раза, то есть существенно разделить на тысячу. t 1/2 — время, по истечении которого количество радиоактивных ядер, присутствующих в образце, уменьшается вдвое, но «срок службы» образца намного превышает его «период полураспада»: радиоактивного вещества всегда остается немного, даже после большое количество «периодов полураспада».
Математически закон распада радиоактивного образца можно охарактеризовать следующим образом:
Математическая характеристика периода полураспада и средней продолжительности жизни
Если N (t) представляет собой количество радионуклидов в момент времени t, то:
- НЕТ(т12)знак равноНЕТ2знак равноНЕТе-λт12знак равноНЕТепер(12){\ displaystyle N (t_ {1/2}) = {\ frac {N_ {0}} {2}} = N_ {0} e ^ {- \ lambda t_ {1/2}} = N_ {0} e ^ {\ ln (1/2)}}
Сразу выводим:
- т12знак равнопер(2)λ{\ displaystyle t_ {1/2} = {\ frac {\ ln (2)} {\ lambda}}}
или же:
- λзнак равнопер(2)т12{\ displaystyle \ lambda = {\ frac {\ ln (2)} {t_ {1/2}}}}
где — количество начальных ядер, — радиоактивная постоянная, соответствующая типу ядер.
НЕТ{\ displaystyle N_ {0}}λ{\ displaystyle \ lambda}
Средняя выживаемость
Период полураспада не следует путать со средней продолжительностью t . Это получается с помощью следующих рассуждений: количество ядер, распадающихся в момент t, «проживало» в течение этого времени t или, точнее, в момент t остается N exp (–λ t) ядер. Из них за период времени уничтожаются:
- dНЕТзнак равноλНЕТexp(-λт)dт{\ displaystyle dN = \ lambda N_ {0} \ exp (- \ lambda t) dt}.
Следовательно, эти dN имеют срок службы от t до t + dt. Таким образом, мы можем определить среднюю продолжительность жизни всех радионуклидов в выборке (или просто среднюю продолжительность жизни ) следующим образом:
- т¯знак равно∫НЕТтdНЕТНЕТ{\ displaystyle {\ overline {t}} = \ int _ {N_ {0}} ^ {0} t {\ frac {dN} {N_ {0}}}}.
Таким образом, учитывая приведенное выше выражение для dN, получаем
- т¯знак равноλ∫+∞тexp(-λт)dтзнак равно1λзнак равнот12пер(2)≈1,44 годт12{\ displaystyle {\ overline {t}} = \ lambda \ int _ {0} ^ {+ \ infty} t \ exp (- \ lambda t) dt = {\ frac {1} {\ lambda}} = {\ гидроразрыв {t_ {1/2}} {\ ln (2)}} \ приблизительно 1 {,} 44 \, t_ {1/2}}.
В научной литературе среднее время жизни радиоактивного вещества обычно обозначается греческой буквой τ, поэтому
- τзнак равнот¯знак равно1λ{\ displaystyle \ tau = {\ overline {t}} = {\ frac {1} {\ lambda}}}.
Этот срок службы не зависит от размера образца ; это характерное время рассматриваемого радионуклида, как и его период полураспада . По истечении этого характерного времени τ активность снижается до доли 1 / e от своего начального значения:
НЕТ{\ displaystyle N_ {0}}т12{\ displaystyle t_ {1/2}}
- НЕТ(τ)знак равноНЕТexp(-λλ)знак равноНЕТе{\ Displaystyle N (\ тау) = N_ {0} \ ехр (- \ lambda / \ lambda) = {\ frac {N_ {0}} {e}}}.
Можно отметить, что это «время жизни» на самом деле является средним временем выживания атома в образце с начала наблюдения . В случае естественного радионуклида его предыдущая жизнь могла быть намного дольше, иногда составляя миллионы лет и более. Символическим примером является Плутоний 244 , с периодом полураспада 80,8 мега- лет, из которых следы атомов , образованных процессов примитивных звездных взрывов задолго до формирования и эволюции системы находятся в почве Земли. Солнечная , так что там больше 5 Гиг- лет. Эти атомы первоначально имели среднюю выживаемость около 80,8 / Ln (2) = 80,8 x 1,4427 млн лет, или 116,7 миллиона лет; но те, кого мы обнаруживаем сегодня — то немногое, что от них осталось — выжили, по крайней мере, в пятьдесят раз больше. Они выжили благодаря удаче; и в среднем их потенциал выживания, отсчитываемый с сегодняшнего дня, составляет 80,8 мега- лет, как в первый день.
Закон радиоактивного распада
Радиоактивность – это способность атомов некоторых веществ превращаться в атомы других веществ с испусканием γ-лучей, а также α- и β- частиц. Такой способностью обладают все элементы с номером 84 и более.
 Рис. 1. Радиоактивность.
Рис. 1. Радиоактивность.
Распад атомов – это случайный процесс, но, если взять большое число атомов, то можно заметить, что скорость распада зависит только от количества атомов в пробе. Например, количество атомов Калия-42 (цифра означает массовое число изотопа) в пробе равно:
|
Часы |
Количество,% |
|
100 |
|
|
6 |
70.7 |
|
12 |
50.0 |
|
18 |
35.4 |
|
24 |
25.0 |
|
30 |
17.7 |
|
36 |
12.5 |
|
42 |
8.8 |
|
48 |
6.3 |
То есть, если массовая доля Калия-42 в пробе изначально была 100г, то за первые шесть часов она уменьшилась на 30г, а за восьмой шестичасовый период – только на 2,5г. Произошло это потому, что в пробе к этому времени стало значительно меньше атомов, скорость распада уменьшилась.
Если взять другое вещество, с другой скоростью распада, например, Йод-124, и замерить массовую долю Йода в пробе в те же моменты, получим следующую таблицу:
|
Часы |
Количество,% |
|
100 |
|
|
6 |
95.8 |
|
12 |
91.7 |
|
18 |
87.8 |
|
24 |
84.1 |
|
30 |
80.5 |
|
36 |
77.1 |
|
42 |
73.8 |
|
48 |
70.7 |
Сравнивая ее с предыдущей, можно отметить, что скорость распада у Йода-124 гораздо меньше, чем у Калия-42, однако, и для этого элемента за первый период распадается большее количество атомов, в последующие периоды – меньшее.
Таким образом, количество нераспавшегося вещества представляет собой бесконечно убывающую геометрическую прогрессию:
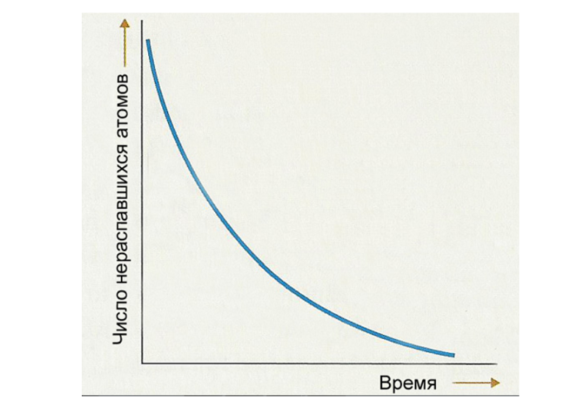 Рис. 2. График радиоактивного распада.
Рис. 2. График радиоактивного распада.
Это степенная функция с отрицательным показателем. В качестве основания функции удобно принять число 2. В результате закон, радиоактивного распада, выражающий, сколько атомов остается в пробе спустя время $t$, выражается формулой:
$$N=N_0×2^{-{1\over T}t},$$
где:
- $t$ – прошедшее время,c;
- $N$ – оставшееся количество атомов;
- $N_0$ – начальное количество атомов в момент $t=0$.
- T – параметр интенсивности (период полураспада),c.
В биологии и фармакологии [ править ]
Биологический период полураспада или период полувыведения — это время, за которое вещество (лекарство, радиоактивный нуклид или другое) теряет половину своей фармакологической, физиологической или радиологической активности. В медицинском контексте период полураспада может также описывать время, которое требуется для того, чтобы концентрация вещества в плазме крови достигла половины его стационарного значения («период полураспада в плазме»).
Взаимосвязь между биологическим периодом полураспада вещества и периодом полураспада в плазме может быть сложной из-за факторов, включая накопление в тканях , активные метаболиты и взаимодействия рецепторов .
В то время как радиоактивный изотоп распадается почти идеально в соответствии с так называемой «кинетикой первого порядка», где константа скорости является фиксированным числом, выведение вещества из живого организма обычно следует более сложной химической кинетике.
Например, биологический период полураспада воды в организме человека составляет от 9 до 10 дней хотя он может изменяться в зависимости от поведения и других условий. Биологический период полураспада цезия в организме человека составляет от одного до четырех месяцев.
Понятие полураспада также используется для пестицидов в растениях , и некоторые авторы утверждают , что модели риска пестицидов и оценки воздействия полагаются на и чувствительны к информации , характеризующей рассеивание из растений.
В эпидемиологии понятие периода полураспада может относиться к промежутку времени, в течение которого количество случаев заболевания в очаге болезни снизится вдвое, особенно если динамику вспышки можно моделировать .
Период полураспада
Как уже было сказано, полоний-210 является очень опасным веществом. Он высокотоксичен, а его период полураспада составляет 138 дней и 9 часов. Под данной величиной подразумевается время, в течение которого вещество распадается примерно в соотношение ½. Применим данный термин, кстати, не ко всем системам. А исключительно к экспоненциально распадающимся.
Важно отметить, что за два таких периода не распадаются все частицы. Ведь каждый этап полураспада уменьшает количество сохранившихся частиц в 2 раза
И еще стоит знать, что активность вещества является пропорциональной количеству его атомов.
Многоликий цезий
В природе цезий встречается исключительно в виде стабильного изотопа Cs-133. Но современная физика знает 39 искусственно созданных радионуклидов (радиоактивных изотопов).
Напомним, что изотопы – это разновидности атома элемента с различным количеством нейтронов в их ядрах.
Дольше всех (до 2,3 миллиона лет) живет изотоп Cs-135, второй по периоду полураспада – цезий-137. Именно последний является виновником радиационного загрязнения нашей планеты. Период полураспада цезия-137 в секундах – 952066726, что составляет 30,17 года.
Данный изотоп образуется при распаде ядер в ядерном реакторе, а также при испытаниях оружия с ядерными боеголовками.

