Закон радиоактивного распада

Закон радиоактивного распада

Любой радионуклидный как вероятно, распадаться в любой момент времени в качестве еще одного радионуклида того же вида, и распад не зависит от физико — химических условий , в которых найден нуклид. Другими словами, распад управляется случайностью, а закон радиоактивного распада — это статистический закон .

NB: в деталях, непрерывные измерения, кажется, показывают вариации радиоактивного распада в зависимости от скорости воздействия нейтрино, которая незначительно меняется в зависимости от положения Земли по отношению к Солнцу.

Если образец радиоактивного материала наблюдается в течение заданного интервала времени, доля ядер, подвергающихся радиоактивному распаду, будет практически постоянной из-за закона больших чисел .

Это показывает , что математически это означает , что число N ядер уменьшается со временем т после экспоненциального распада  : . Это демонстрируется следующим образом:
НЕТ(т)знак равноНЕТе-λт{\ Displaystyle N (T) = N_ {0} \, e ^ {- \ lambda t}}

Математическая демонстрация экспоненциального закона

Пусть Н ( т ) быть количество радионуклидов одного данного химического элемента , присутствующего в образце , в любой момент времени т . Поскольку вероятность распада одного из этих радионуклидов не зависит ни от присутствия других радионуклидов, ни от окружающей среды, общее количество распадов –d N за небольшой интервал времени d t ( N уменьшается со временем: d N — изменение числа N (d N <0), количество недостающих ядер равно –d N ) пропорционально количеству радионуклидов N, присутствующих в момент времени t, и продолжительности d t этого интервала:

-dНЕТзнак равноλНЕТdт{\ displaystyle — \ mathrm {d} N = \ lambda N \, \ mathrm {d} t}

где коэффициент пропорциональности λ , называемый радиоактивной постоянной рассматриваемого радионуклида, имеет размерность, обратную времени; постоянная λ положительна.

Интегрируя предыдущее дифференциальное уравнение, мы находим число N ( t ) радионуклидов, присутствующих в организме в любой момент t , зная, что в данный момент t = 0 их было N  ; это экспоненциальный закон затухания

НЕТ(т)знак равноНЕТе-λт{\ Displaystyle N (T) = N_ {0} \, e ^ {- \ lambda t}}

или же :

• N — начальное количество неразложившихся ядер;
• λ — радиоактивная постоянная элемента.

Однако следует отметить, что этот закон уменьшения касается только радиоактивности, вызванной исходным радионуклидом  ; но радионуклиды, образующиеся в результате радиоактивного распада исходного радионуклида, могут сами быть радиоактивными и вызывать свою собственную радиоактивность. В этом случае их радиоактивность постепенно добавляется к радиоактивности исходного радионуклида. Активность смеси, созданной таким образом между исходным радионуклидом и его потомком (ями), обсуждается в разделе «Филиализация двух зависимых изотопов» ниже.

Бета-распад

В процессе бета-распада ядро испускает электрон. Вообще существование в ядре электрона невозможно, т.е. появление электрона – лишь результат β-распада, сопровождающегося превращением нейтрона в протон. Такой процесс происходит как внутри ядра, так и со свободными нейтронами. Среднее время жизни свободного нейтрона равно примерно 15 минутам. При радиоактивном распаде нейтрон n1 превращается в протон p11 и электрон e-1.

В результате измерений было выявлено, что при бета-распаде наблюдается кажущееся нарушение закона сохранения энергии, поскольку суммарно энергия протона и электрона, появившихся при распаде нейтрона, меньше энергии нейтрона. В 1931 году В. Паули предположил выделение при распаде нейтрона еще одной частицы с нулевыми значениями массы и заряда, уносящей с собой часть энергии.

Определение 6

Нейтрино (маленький нейтрон) – частица с нулевыми значениями массы и заряда, возникающая при распаде нейтрона. Была открыта в 1953 году.

Нейтрино плохо взаимодействует с атомами вещества, поскольку не обладает зарядом и массой, и вследствие этого ее обнаружение в ходе эксперимента очень затруднительно. Ионизирующая способность нейтрино является настолько малой, что один акт ионизации в воздухе приходится приблизительно на 500 км пути. На данный момент известно, что существует несколько типов нейтрино.

Определение 7

Электронный антинейтрино – частица, возникающая вследствие распада нейтрона и обозначаемая ve~.

Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!

Описать задание

Запись реакции распада нейтрона выглядит так:

n1→p11+e-1+ve~

Те же явления происходят внутри ядер при β-распаде. При распаде одного их ядерных нейтронов образуется электрон, сразу же выбрасываемый из «родительского дома» (ядра) с очень большой скоростью, отличающейся от скорости света на небольшую долю процента. Поскольку распределение энергии, выделяющейся при β-распаде, между электроном, нейтрино и дочерним ядром имеет случайный характер, β-электроны способны обладать разными скоростями в широком интервале значений.

β-распад сопровождается увеличением зарядового числа Z на единицу при неизменности массового числа A. Дочернее ядро в данном случае есть ядро одного из изотопов элемента, чей атомный номер в периодической системе Менделеева на единицу превышает атомный номер исходного ядра. В качестве характерного примера β-распада можно рассмотреть преобразование изотона тория Th90234, возникающего при α-распаде урана U92238, в протактиний Pa91234:

Th90234→Pa91234+e-1+ve~

Совместно с электронным β-распадом было определено такое явление, как позитронный β+-распад: ядро испускает позитронe+1 и нейтрино ve.

Определение 8

Позитрон является частицей-двойником электрона, отличающейся от него лишь знаком заряда.

Существование позитрона предсказывалось еще в 1928 г. великим физиком П. Дираком. Спустя несколько лет позитрон обнаружили, как составляющую космических лучей. Позитроны возникают в результате реакции преобразования протона в нейтрон по следующей схеме:

p11→n1+e1+ve

Период полураспада радиоактивного вещества

«  Период полураспада  » или период полураспада радиоактивного изотопа — это время, по истечении которого количество ядер этого изотопа, присутствующих в образце, уменьшается вдвое. Обычно обозначается буквой T или t _½ .

Если мы наблюдаем образец радиоактивного материала, через время t _1/2 , этот образец (по определению) потеряет половину своего материала, и останется только половина исходного материала. Но по истечении этого времени дважды потеря дополнительного материала относится только к оставшейся половине, а не к исходной сумме; после двойного t _½ останется половина половины исходного материала, то есть четверть. Точно так же после трехкратного увеличения t _½ останется только (1/2) 3 = 1/8 первоначальной выборки и так далее. После того, как этот период полураспада будет увеличиваться в десять раз, активность снизится в 2 10 = 1024 раза, то есть существенно разделить на тысячу. t _1/2 — время, по истечении которого количество радиоактивных ядер, присутствующих в образце, уменьшается вдвое, но «срок службы» образца намного превышает его «период полураспада»: радиоактивного вещества всегда остается немного, даже после большое количество «периодов полураспада».

Математически закон распада радиоактивного образца можно охарактеризовать следующим образом:

Математическая характеристика периода полураспада и средней продолжительности жизни

Если N (t) представляет собой количество радионуклидов в момент времени t, то:

НЕТ(т12)знак равноНЕТ2знак равноНЕТе-λт12знак равноНЕТепер⁡(12){\ displaystyle N (t_ {1/2}) = {\ frac {N_ {0}} {2}} = N_ {0} e ^ {- \ lambda t_ {1/2}} = N_ {0} e ^ {\ ln (1/2)}}

Сразу выводим:

т12знак равнопер⁡(2)λ{\ displaystyle t_ {1/2} = {\ frac {\ ln (2)} {\ lambda}}}

или же:

λзнак равнопер⁡(2)т12{\ displaystyle \ lambda = {\ frac {\ ln (2)} {t_ {1/2}}}}

где — количество начальных ядер, — радиоактивная постоянная, соответствующая типу ядер.
НЕТ{\ displaystyle N_ {0}}λ{\ displaystyle \ lambda}

Средняя выживаемость

Период полураспада не следует путать со средней продолжительностью t . Это получается с помощью следующих рассуждений: количество ядер, распадающихся в момент t, «проживало» в течение этого времени t или, точнее, в момент t остается N exp (–λ t) ядер. Из них за период времени уничтожаются:

dНЕТзнак равноλНЕТexp⁡(-λт)dт{\ displaystyle dN = \ lambda N_ {0} \ exp (- \ lambda t) dt}.

Следовательно, эти dN имеют срок службы от t до t + dt. Таким образом, мы можем определить среднюю продолжительность жизни всех радионуклидов в выборке (или просто среднюю продолжительность жизни ) следующим образом:

т¯знак равно∫НЕТтdНЕТНЕТ{\ displaystyle {\ overline {t}} = \ int _ {N_ {0}} ^ {0} t {\ frac {dN} {N_ {0}}}}.

Таким образом, учитывая приведенное выше выражение для dN, получаем

т¯знак равноλ∫+∞тexp⁡(-λт)dтзнак равно1λзнак равнот12пер⁡(2)≈1,44 годт12{\ displaystyle {\ overline {t}} = \ lambda \ int _ {0} ^ {+ \ infty} t \ exp (- \ lambda t) dt = {\ frac {1} {\ lambda}} = {\ гидроразрыв {t_ {1/2}} {\ ln (2)}} \ приблизительно 1 {,} 44 \, t_ {1/2}}.

В научной литературе среднее время жизни радиоактивного вещества обычно обозначается греческой буквой τ, поэтому

τзнак равнот¯знак равно1λ{\ displaystyle \ tau = {\ overline {t}} = {\ frac {1} {\ lambda}}}.

Этот срок службы не зависит от размера образца  ; это характерное время рассматриваемого радионуклида, как и его период полураспада . По истечении этого характерного времени τ активность снижается до доли 1 / e от своего начального значения:
НЕТ{\ displaystyle N_ {0}}т12{\ displaystyle t_ {1/2}}

НЕТ(τ)знак равноНЕТexp⁡(-λλ)знак равноНЕТе{\ Displaystyle N (\ тау) = N_ {0} \ ехр (- \ lambda / \ lambda) = {\ frac {N_ {0}} {e}}}.

Можно отметить, что это «время жизни» на самом деле является средним временем выживания атома в образце с начала наблюдения . В случае естественного радионуклида его предыдущая жизнь могла быть намного дольше, иногда составляя миллионы лет и более. Символическим примером является Плутоний 244 , с периодом полураспада 80,8 мега- лет, из которых следы атомов , образованных процессов примитивных звездных взрывов задолго до формирования и эволюции системы находятся в почве Земли. Солнечная , так что там больше 5 Гиг- лет. Эти атомы первоначально имели среднюю выживаемость около 80,8 / Ln (2) = 80,8 x 1,4427 млн ​​лет, или 116,7 миллиона лет; но те, кого мы обнаруживаем сегодня — то немногое, что от них осталось — выжили, по крайней мере, в пятьдесят раз больше. Они выжили благодаря удаче; и в среднем их потенциал выживания, отсчитываемый с сегодняшнего дня, составляет 80,8 мега- лет, как в первый день.

Характеристики распада[править | править код]

Наглядная демонстрация закона.

Кроме константы распада λ,{\displaystyle \lambda ,} радиоактивный распад характеризуют ещё двумя производными от неё константами, рассмотренными ниже.

Среднее время жизниправить | править код

Из закона радиоактивного распада можно получить выражение для среднего времени жизни радиоактивного атома. Число атомов, в момент времени t{\displaystyle t} претерпевших распад в пределах интервала dt{\displaystyle dt} равно −dN,{\displaystyle -dN,} их время жизни равно −tdN.{\displaystyle -tdN.} Среднее время жизни получаем интегрированием по всему периоду распада:

τ=−1N∫NtdN=λ∫∞te−λtdt=1λ.{\displaystyle \tau =-{\frac {1}{N_{0}}}\int _{N_{0}}^{0}tdN=\lambda \int _{0}^{\infty }te^{-\lambda t}dt={\frac {1}{\lambda }}.}

Подставляя эту величину в экспоненциальные временные зависимости для N(t){\displaystyle N(t)} и I(t),{\displaystyle \mathrm {I} (t),} легко видеть, что за время τ{\displaystyle \tau } число радиоактивных атомов и активность образца (количество распадов в секунду) уменьшаются в e раз.

Период полураспадаправить | править код

На практике получила большее распространение другая временная характеристика — период полураспада T12,{\displaystyle T_{1/2},} равная времени, в течение которого число радиоактивных атомов или активность образца уменьшаются в 2 раза.

Связь этой величины с постоянной распада можно вывести из соотношения N(T12)N=e−λT12=12,{\displaystyle {\frac {N(T_{1/2})}{N_{0}}}=e^{-\lambda T_{1/2}}=1/2,} откуда:

T12=ln⁡2λ=τln⁡2≈,693τ.{\displaystyle T_{1/2}={\frac {\ln 2}{\lambda }}=\tau \ln 2\approx 0,693\tau .}

Примеры характеристик распада[править | править код]

Существующие в природе радиоактивные изотопы в основном возникают в сложных цепочках распадов урана и тория и имеют периоды полураспада в очень широкой области значений: от 3⋅10−7 секунды для 212Po до 1,4⋅1010 лет для 232Th. Наибольший экспериментально измеренный период полураспада имеет изотоп теллура 128Te — 2,2⋅1024 лет. Само существование в настоящее время многих естественных радиоактивных элементов несмотря на то, что с момента образования этих элементов при звёздном нуклеосинтезе прошло более 4,5 млрд лет, является следствием очень больших периодов полураспада 235U, 238U, 232Th и других природных радионуклидов. К примеру, изотоп 238U стоит в начале длинной цепочки (так называемый ), состоящей из 20 изотопов, каждый из которых возникает при α-распаде или β-распаде предыдущего элемента. Период полураспада 238U (4,5⋅109 лет) много больше, чем период полураспада любого из последующих элементов радиоактивного ряда, поэтому распад в целом всей цепочки происходит за то же время, что и распад 238U, её родоначальника, в таких случаях говорят, что цепочка находится в состоянии секулярного (или векового) равновесия. Примеры характеристик распада некоторых веществ:

Вещество	238U	235U	234U	210Bi	210Tl
Период полураспада, T12{\displaystyle T_{1/2}}	4,5⋅109 лет	7,13⋅108 лет	2,48⋅105 лет	4,97 дня	1,32 минуты
Постоянная распада, λ{\displaystyle \lambda }	4,84⋅10−18 с−1		8,17⋅10−14 с−1	1,61⋅10−6с−1	8,75⋅10−3 с−1
Частица	α	α	α	β	β
Полная энергия распада, МэВ	4,2699	4,6780	4,8575	1,1612	5,482

Период полураспада

2. В любом образце радиоактивного вещества находится огромное число ядер. В процессе радиоактивного распада число ядер со временем уменьшается, однако предсказать, когда именно — через секунду, месяц или тысячу лет — распадётся то или иное ядро, невозможно. Распад каждого ядра является совершенно случайным событием; данный процесс носит, как говорят, вероятностный, статистический характер. Бессмысленно поэтому говорить о времени жизни одного какого-либо атома. Когда используется этот термин, то имеют в виду некоторое среднее значение, измеренное для очень большого числа атомов данного вещества.

Физической величиной, характеризующей интенсивность радиоактивного распада, принято считать интервал времени, равный периоду полураспада.

Период полураспада Т — это время, в течение которого распадается половина первоначального числа радиоактивных ядер.

Для каждого радиоактивного вещества период полураспада является строго постоянной величиной. Например, у изотопа свинца период полураспада составляет 1,43 • 1017 лет, а у изотопа радиоактивного газа радона он равен всего лишь 10-6 с.

Опыты с радиоактивными веществами показали, что никакие внешние условия, такие как изменение агрегатного состояния, нагревание до высоких температур или охлаждение до сверхнизких температур, большие давления и пр., не влияют на характер и скорость радиоактивного распада.

Характеристики распада

Наглядная демонстрация закона.

Кроме константы распада λ,{\displaystyle \lambda ,} радиоактивный распад характеризуют ещё двумя производными от неё константами, рассмотренными ниже.

Среднее время жизни

Из закона радиоактивного распада можно получить выражение для среднего времени жизни радиоактивного атома. Число атомов, в момент времени t{\displaystyle t} претерпевших распад в пределах интервала dt{\displaystyle dt} равно −dN,{\displaystyle -dN,} их время жизни равно −tdN.{\displaystyle -tdN.} Среднее время жизни получаем интегрированием по всему периоду распада:

τ=−1N∫NtdN=λ∫∞te−λtdt=1λ.{\displaystyle \tau =-{\frac {1}{N_{0}}}\int _{N_{0}}^{0}tdN=\lambda \int _{0}^{\infty }te^{-\lambda t}dt={\frac {1}{\lambda }}.}

Подставляя эту величину в экспоненциальные временные зависимости для N(t){\displaystyle N(t)} и I(t),{\displaystyle \mathrm {I} (t),} легко видеть, что за время τ{\displaystyle \tau } число радиоактивных атомов и активность образца (количество распадов в секунду) уменьшаются в e раз.

Период полураспада

На практике получила большее распространение другая временная характеристика — период полураспада T12,{\displaystyle T_{1/2},} равная времени, в течение которого число радиоактивных атомов или активность образца уменьшаются в 2 раза.

Связь этой величины с постоянной распада можно вывести из соотношения N(T12)N=e−λT12=12,{\displaystyle {\frac {N(T_{1/2})}{N_{0}}}=e^{-\lambda T_{1/2}}=1/2,} откуда:

T12=ln⁡2λ=τln⁡2≈,693τ.{\displaystyle T_{1/2}={\frac {\ln 2}{\lambda }}=\tau \ln 2\approx 0,693\tau .}

Альфа-распад

Определение 4

Альфа-распад – это самопроизвольное преобразование атомного ядра с числом протонов Z и нейтронов N в иное (дочернее) ядро, в котором содержится число протонов Z–2 и нейтронов N–2, сопровождающееся испусканием α-частицы – ядра атома гелия He24.

Пример 1

Образцом альфа-распада может служить α-распад радия: 

Ra88226→Rn86222+He24

α-частицы, которые испускают ядра атомов радия, Резерфорд применял, проводя экспериментальное рассеивание на ядрах тяжелых элементов. Измерение по кривизне траектории в магнитном поле установило скорость α-частиц, испускаемых при α-распаде ядер радия: порядка 1,5·107 мс. Размер кинетической энергии при этом — примерно 7,5·10–13 Дж (около 4,8 МэВ). Эта величина несложно определяется, когда известны значения масс материнского и дочернего ядер и ядра гелия. Скорость испускаемой α-частицы очень велика, однако она равна лишь 5 % от скорости света, т.е. в расчетах допустимо использовать нерелятивистское выражение для кинетической энергии.

Также результатом исследований стал факт, что радиоактивное вещество способно испускатьα-частицы с несколькими дискретными значениями энергий. Объяснение этому явлению заключается в способности ядер находиться, аналогично атомам, в различных возбужденных состояниях. В одном из таких состояний может оказаться дочернее ядро при α-распаде. Далее ядро переходит в основное состояние, и испускается γ-квант. Схема α-распада радия с испусканием α-частиц с двумя значениями кинетических энергий указана на рис. 6.7.2.

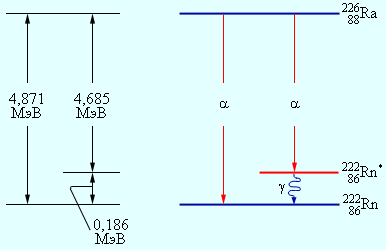
Рисунок 6.7.2. Энергетическая диаграмма α-распада ядер радия. Продемонстрировано возбужденное состояние ядра радона Rn*86222. При переходе из возбужденного состояния ядра радона в основное происходит излучение γ-кванта с энергией ,186 МэВ.

Итак, α-распад ядра во множестве случаев происходит совместно с γ-излучением.

Теория α-распада также содержит предположение о возможном образовании ядер групп, включающих в себя два протона и два нейтрона, т. е. α-частицу. Материнское ядро служит для α-частиц потенциальной ямой, ограниченной потенциальным барьером. Количество энергии α-частицы в ядре не хватает, чтобы преодолеть данный барьер (рис. 6.7.3).

Определение 5

Испускание α-частицы из ядра возможно лишь благодаря такому квантово-механическому явлению, как туннельный эффект.

Квантовая механика гласит, что существует неравная нулю вероятность прохождения частицы под потенциальным барьером. Явление туннелирования носит вероятностный характер.

Рисунок 6.7.3. Туннелирование α-частицы сквозь потенциальный барьер.

Интенсивность радиоактивного распада

В опытах с радиоактивностью Э.Резерфорда и Ф Содди было обнаружено, что хотя радиоактивность тория в запаянной ампуле постоянна, если ампулу разбить, то радиоактивность заметно снижается.

Было предположено, что торий при распаде выделяет какой-то газ, который также является радиоактивным, и радиоактивность которого гораздо больше, чем самого тория, он и дает основной вклад в активность пробы. Газ, откачиваемый из ампулы с торием, действительно был более радиоактивным, но его радиоактивность очень быстро уменьшалась. Уже через несколько минут она падала в несколько раз. Однако, выделенный газ удалось исследовать. Он оказался инертным газом с порядковым номером 86 (радон).

Доля атомов, распадающихся в единицу времени, для каждого радиоактивного вещества постоянна.

Например, если за пять минут распадается 10% имеющейся радиоактивной пробы, то за следующие пять минут распадется еще 10% от оставшейся пробы, и так далее. Если измерять количество такого радиоактивного вещества через каждые пять минут, мы получим значения:

Время, мин	Количество,%
100.00
5	90.00
10	81.00
15	72.90
20	65.61
25	59.05
30	53.14

Можно видеть, что количество остающегося радиоактивного вещества представляет собой бесконечно убывающую геометрическую прогрессию. График количества вещества:

Рис. 3. График радиоактивного распада

То есть, закон радиоактивного распада представляет собой степенную функцию с отрицательным показателем. В качестве основания функции удобно принять число 2. В результате имеем следующую формулу закона радиоактивного распада, показывающую, сколько атомов вещества останется в пробе спустя время t:

$$N=N_0×2^{-{1\over T}t},$$

где:

• $t$ – прошедшее время,c;
• $N$ – оставшееся количество атомов вещества;
• $N_0$ – начальное количество атомов вещества в момент $t=0$.
• T – параметр интенсивности (период полураспада),c.

Параметр T, представляет собой время, за которое распадется половина исходного вещества. Поэтому он называется периодом полураспада.

Распад каждого отдельного атома – это случайный процесс. Невозможно предсказать, когда атом распадется, он не имеет «возраста». В большом количестве атомов за время полураспада распадется половина атомов. Но среди них будут такие, что распадутся почти сразу, а будут и «долгожители», которые распадутся значительно позже.

Что мы узнали?

Согласно закону радиоактивного распада, доля атомов вещества, распадающегося за единицу времени, для данного элемента постоянна. Время, за которое распадается половина атомов, называется периодом полураспада. Он является параметром интенсивности распадов.

1. /10

   Вопрос 1 из 10

Примеры характеристик распада[править | править код]

Существующие в природе радиоактивные изотопы в основном возникают в сложных цепочках распадов урана и тория и имеют периоды полураспада в очень широкой области значений: от 3⋅10−7 секунды для 212Po до 1,4⋅1010 лет для 232Th. Наибольший экспериментально измеренный период полураспада имеет изотоп теллура 128Te — 2,2⋅1024 лет. Само существование в настоящее время многих естественных радиоактивных элементов несмотря на то, что с момента образования этих элементов при звёздном нуклеосинтезе прошло более 4,5 млрд лет, является следствием очень больших периодов полураспада 235U, 238U, 232Th и других природных радионуклидов. К примеру, изотоп 238U стоит в начале длинной цепочки (так называемый ), состоящей из 20 изотопов, каждый из которых возникает при α-распаде или β-распаде предыдущего элемента. Период полураспада 238U (4,5⋅109 лет) много больше, чем период полураспада любого из последующих элементов радиоактивного ряда, поэтому распад в целом всей цепочки происходит за то же время, что и распад 238U, её родоначальника, в таких случаях говорят, что цепочка находится в состоянии секулярного (или векового) равновесия. Примеры характеристик распада некоторых веществ:

Вещество	238U	235U	234U	210Bi	210Tl
Период полураспада, T12{\displaystyle T_{1/2}}	4,5⋅109 лет	7,13⋅108 лет	2,48⋅105 лет	4,97 дня	1,32 минуты
Постоянная распада, λ{\displaystyle \lambda }	4,84⋅10−18 с−1		8,17⋅10−14 с−1	1,61⋅10−6с−1	8,75⋅10−3 с−1
Частица	α	α	α	β	β
Полная энергия распада, МэВ	4,2699	4,6780	4,8575	1,1612	5,482

Закон радиоактивного распада

Радиоактивный распад отдельного ядра является совершенно случайным событием. Однако для каждого радиоактивного вещества существует характерный интервал времени, называемый периодом полураспада.

Период полураспада — промежуток времени, за который распадается ровно половина всех ядер.

К примеру, если в некоторый момент времени вещество состоит из N ядер, то через время T, равное периоду полураспада ядер, останется N/2 ядер. В таком случае, через время, равное 2T останется еще вдвое меньше ядер — N/2. И т.д.

Эту закономерность можно записать в виде формулы, которая получила название закона радиоактивного распада:

N=N·2−tT..

N — число ядер в момент времени t, N— исходное число ядер, T — период полураспада.

Период полураспада зависит от рода вещества. У урана 238.92U он составляет 4,5 млрд лет. У радия — 1,6 тыс. лет. Существуют химические элементы с периодом полураспада, составляющим миллионные доли секунды.

Пример №2. Период полураспада радия составляет 1600 лет. Через какое время число атомов уменьшится в 4 раза?

Для вычислений применим формулу:

N=N·2−tT..

Известно, что:

N=4N

Следовательно:

N=4N·2−tT..

1=4·2−tT..

14..=2−tT..

2−2=2−tT..

−tT..=−2

По условию задачи период полураспада равен 1600. Следовательно:

−t1600..=−2

t=2·1600=3200(лет)

Радиоактивный распад

Радиоактивность была случайно открыта А. Беккерелем, который исследовал послесвечение солей урана. Оказалось, что соли засвечивают фотопластинку даже тогда, когда проба не подвергалась освещению.

Заинтересовавшись обнаруженным явлением, Беккерель открыл, что атомы урана действительно испускают невидимые лучи. Способность испускать такие лучи была названа радиоактивностью. Радиоактивными оказались все элементы с порядковым номером более 83.

Рис. 1. Радиоактивные элементы.

Но, наиболее удивительным в радиоактивных веществах было то, что любое из радиоактивных веществ со временем превращается совсем в другие вещества, существенно отличающиеся от первоначальных по физическим и химическим свойствам. Количество же исходной пробы при этом уменьшается.

Стало ясно, что радиоактивные элементы способны к самопроизвольным превращениям. И поскольку продукт этого превращения всегда был легче, чем первоначальный элемент, это превращение было названо радиоактивным распадом.

Рис. 2. Распад ядра.

Экспоненциальный закон[править | править код]

Экспоненциальная кривая радиоактивного распада: по оси абсцисс («оси x») — нормированное время Θ=tτ,{\displaystyle \Theta =t/\tau ,} по оси ординат («оси y») — доля NN{\displaystyle N/N_{0}} ещё нераспавшихся ядер или скорость распада в единицу времени I(τ)=dNdΘ{\displaystyle \mathrm {I} (\tau )=dN/d\Theta }

В указанном выше математическом выражении неотрицательная константа λ{\displaystyle \lambda } — постоянная распада, которая характеризует вероятность радиоактивного распада за единицу времени и имеющая размерность с−1. Знак минус указывает на убыль числа радиоактивных ядер со временем.

Решение этого дифференциального уравнения имеет вид:

N(t)=Ne−λt,{\displaystyle N(t)=N_{0}e^{-\lambda t},}

где N{\displaystyle N_{0}} — начальное число атомов, то есть число атомов для t={\displaystyle t=0.}

Таким образом, число радиоактивных атомов уменьшается со временем по экспоненциальному закону. Скорость распада, то есть число распадов в единицу времени:

I(t)=−dNdt,{\displaystyle \mathrm {I} (t)=-{\frac {dN}{dt}},}

также падает экспоненциально. Дифференцируя выражение для зависимости числа атомов от времени, получаем:

I(t)=−ddt(Ne−λt)=λNe−λt=Ie−λt,{\displaystyle \mathrm {I} (t)=-{\frac {d}{dt}}(N_{0}e^{-\lambda t})=\lambda N_{0}e^{-\lambda t}=\mathrm {I} _{0}e^{-\lambda t},}

где I{\displaystyle \mathrm {I} _{0}} — скорость распада в начальный момент времени t={\displaystyle t=0.}

Таким образом, зависимость от времени числа нераспавшихся радиоактивных атомов и скорости распада описывается одной и той же постоянной λ{\displaystyle \lambda }.