Время, скорость, расстояние

Примеры решения задач

Пример

Задание. Траектория движения материальной точки изображена на рис. 1. Каков путь, пройденный точкой,
чему равно перемещение, если точка двигалась 1-2-3-4.

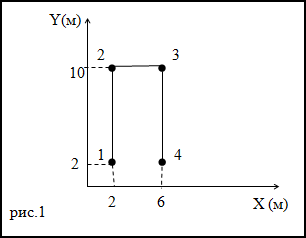
Решение. Перемещение – кратчайшее расстояние между точками 1 и 4. Следовательно, перемещение точки равно:

$$6 — 2 = 4 (m)$$

Путь – длина траектории. Рассматривая график на рис.1 получаем, что путь материальной точки равен:

$$8 + 4 + 8 = 20 (m)$$

Ответ. Путь равен 20 м, перемещение равно 4 м.

Слишком сложно?

Формула пути не по зубам? Тебе ответит эксперт через 10 минут!

Пример

Задание. Уравнение движения материальной точки в прямоугольной декартовой системе координат представлено функцией:
x=-0,2t2 (м) . Какой путь пройдет материальная точка за 5 с?

Решение. Так как уравнение движения задано только одной координатой, то в качестве основы для решения
задачи примем формулу пути в виде:

$$s=\int_{t_{1}}^{t_{2}} \sqrt{(\dot{x})^{2}} d t(2.1)$$

Подставим в (2.1) функцию x=-0,2t2, учтем, что $0 c \leq t \leq 5 c$ имеем:

$$s=\int_{0}^{5} \sqrt{\left(-0,2 \frac{d\left(t^{2}\right)}{d t}\right)^{2}} d t=0,\left.4 \cdot \frac{t^{2}}{2}\right|_{0} ^{5}=5(m)$$

Ответ. s=5м.

Читать дальше: Формула равноускоренного движения.

1.4. Разведка целей и их оценка

Разведка целей и их оценка организуется командиром подразделения еще при организации боя и непрерывно продолжаются и в ходе его ведения.

Цели на поле боя могут быть неподвижными, появляющимися на короткое время и движущимися.

В бою огонь ведется, как правило, в составе подразделения, при этом уничтожаются цели, указанные командиром. Поэтому стрелок должен внимательно слушать и точно выполнять все команды.

Если ему цель для поражения не указана, он выбирает ее сам.

При оценке важности и определении очередности поражения цели командир должен исходить из того, какой ущерб в бою эта цель по своим огневым возможностям способна нанести. Важными целями считаются такие, поражение которых в данных условиях обстановки может облегчить и ускорить выполнение боевой задачи

Важными целями считаются такие, поражение которых в данных условиях обстановки может облегчить и ускорить выполнение боевой задачи.

Важными целями обычно являются огневые средства противника: танки, БТР, САУ, ПТУР, пулеметы, гранатометы, наблюдательные пункты, радиолокационные станции и т. д.

В том случае, когда эти цели находятся от подразделения в пределах их дальности действительного огня, они называются опасными.

Особо опасными целями во всех случаях являются средства ядерного нападения противника – пусковые установки и орудия, применяющие ядерные боеприпасы.

Те важные цели, которые находится на расстояниях, превышающих их дальность действительного огня, считается не опасными в данный момент боя.

Деление целей на важные и менее важные, опасные и неопасные позволяет командиру быстро и правильно принимать решение по очередности их поражения; в первую очередь должны уничтожаться опасные цели, во вторую очередь — важные цели, а затем — все остальные.

Из двух равных по важности целей следует выбирать для обстрела ближайшую и наиболее уязвимую, а при появлении во время стрельбы новой, более важной цели немедленно перенести огонь на нее

Формы площади горения

Какие бывают формы пожара – вопрос, который требует более детального разъяснения. Начинать надо с того, что форма сама зависит от нескольких факторов. А именно:

• места возникновения очага возгорания;
• вида материалов, которые горят;
• объемно-планировочной схемы здания или сооружения;
• архитектурных характеристик постройки;
• метеорологических условий, действующих во время чрезвычайной ситуации.

Это не полный список, но именно эти факторы учитываются при расчете.

Итак, существует три вида форм площадей пожара: круглая, угловая и прямоугольная. Надо отметить, что такое обозначение является все-таки условным. Но они закладываются в основу расчетов только из-за простоты проведения этих расчетов. Других причин нет.

Круглая форма

Что значит, круглая форма площади пожара. Это когда огонь распространяется во все стороны равномерно с одинаковой скоростью. При этом пламя не встречает серьезных препятствий. Обычно такие формы, кстати, относящиеся к категории простых, появляются на больших ничем не ограниченных площадях, где не действуют серьезные метеорологические условия. К примеру, на полях пшеницы в безветрие, внутри складов для хранения пиломатериалов и так далее.

Круглая форма площади пожара

Из курса школьной геометрии площадь круга имеет определенную формулу:

S=πR², где R – это путь, пройденный огнем в одну сторону от центра очага возгорания. Нередко в формулах его обозначают буквой «L». То есть определить площадь тушения пожара круглой формы можно именно по этой формуле.

Угловая

Эта конфигурация появляется в двух случаях:

1. Когда на границе участка с пожарной нагрузкой располагаются конструкции из негорючих или слабогорючих материалов, к примеру, в складе в самом углу помещения. В этом случае огонь распространяется в сторону от границ (от стен).
2. На открытой местности при ветреной погоде. Куда дует ветер, туда и распространяется огонь. То есть движение пламени происходит в одном направлении, образуя угловую конфигурацию.

При этом сама форма может иметь три вариации:

• острую, то есть меньше 90°;
• тупую – больше 90°;
• прямую — 90°.

Разновидности угловых форм распространения огня

Первая разновидность встречается редко. Чаще огонь распространяется под углом 90, 180 или 270°. Можно добавить, что круглая конфигурация площади тушения пожара является производной от угловой вариации с углом распространения огня 360°.

Если говорить о формулах площади пожара углового типа, то в них закладывается именно величина угла. Вот три формулы:

1. S=πR²/4 – это для угла 90°.
2. S=πR²/2 – это для угла 180°.
3. S=3πR²/4 – для угла величиной 270°.

Внутри зданий иногда встречаются помещения (очень редко), в которых конфигурация не является прямоугольной. Тогда для проведения расчетов площади пожара используют ниже следующую формулу:

S=απR²/360°. Здесь α – это угол распространения огня, не кратный 90.

Угловое распространение огня

Прямоугольная

Обычно эта форма появляется на ограниченных участках. При этом границы собой представляют конструкции, возведенные из негорючих материалов. А так как здания и сооружения возводятся в виде прямоугольников, то и распространение огня происходит по этой форме. Отсюда и название.

При этом распространяться огонь может в разных направлениях с разной скоростью. То есть с ветреной стороны быстрее, с подветренной слабее. Или, как вариант, одинаковая скорость во всех направлениях в безветренную погоду. Обычно в зданиях с небольшой площадью форму очаг возгорания принимает уже на стадии возникновения.

Что касается формулы расчета, то она одинакова для всех вариантов, только в них добавляется значение распространения огня: в одну или две стороны. Но фото ниже это хорошо видно. Вот эта формула:

S=a x b, где «a» и «b» — стороны прямоугольника.

Если распространение происходит в одну сторону, то формула не изменяется, потому что длина одной из границ составляет путь, который проходит огонь. В том случае, если распространение пламени от центра очага возгорания происходит в две противоположные стороны, то для расчета берется видоизмененная формула, в которой значение «b» — это две длины распространения огня.

Прямоугольная конфигурация площади очага возгорания

ФИЗИКА

§ 8. Перемещение тела при прямолинейном равноускоренном движении без начальной скорости

Рассмотрим, как рассчитывается проекция вектора перемещения тела, движущегося равноускоренно, если его начальная скорость v равна нулю. В этом случае уравнение

будет выглядеть так:

Перепишем это уравнение, подставив в него вместо проекций s_x и а_х модули s и a векторов

перемещения и ускорения. Поскольку в данном случае векторы sua направлены в одну сторону, их проекции имеют одинаковые знаки. Поэтому уравнение для модулей векторов можно записать:

Из этой формулы следует, что при прямолинейном равноускоренном движении без начальной скорости модуль вектора перемещения прямо пропорционален квадрату промежутка времени, в течение которого это перемещение было совершено. Это означает, что при увеличении в n раз времени движения (отсчитываемого от момента начала движения) перемещение увеличивается в n2 раз.

Например, если за произвольный промежуток времени t₁ от начала движения тело совершило перемещение

то за промежуток времени t₂ = 2t₁ (отсчитываемый от того же момента, что и t₁) оно совершит перемещение

за промежуток времени t_n = nt_l — перемещение s_n = n2s_l (где n — натуральное число).

Эта зависимость модуля вектора перемещения от времени при прямолинейном равноускоренном движении без начальной скорости наглядно отражена на рисунке 15, где отрезки ОА, OB, ОС, OD и ОЕ представляют собой модули векторов перемещений (s₁, s₂, s₃, s₄ и s₅), совершённых телом соответственно за промежутки времени t₁, t₂ = 2t₁, t₃ = 3t₁, t₄ = 4t₁ и t₅ = 5t₁.

Рис. 15. Закономерности равноускоренного движения: ОА:ОВ:ОС:OD:0E = 1:4:9:16:25; OA:AB:BC:CD:DE = 1:3:5:7:9

Из этого рисунка видно, что

ОА:ОВ:ОС:OD:ОЕ = 1:4:9:16:25, (1)

т. е. при увеличении промежутков времени, отсчитываемых от начала движения, в целое число раз по сравнению с t₁, модули соответствующих векторов перемещений возрастают как ряд квадратов последовательных натуральных чисел.

Из рисунка 15 видна ещё одна закономерность:

ОА:АВ:ВС:CD:DE = 1:3:5:7:9, (2)

т. е. модули векторов перемещений, совершаемых телом за последовательные равные промежутки времени (каждый из которых равен t₁), относятся как ряд последовательных нечётных чисел.

Закономерности (1) и (2) присущи только равноускоренному движению. Поэтому ими можно пользоваться, если необходимо определить, является движение равноускоренным или нет.

Определим, например, было ли равноускоренным движение улитки, которая за первые 20 с движения переместилась на 0,5 см, за вторые 20 с — на 1,5 см, за третьи 20 с — на 2,5 см.

Для этого найдём, во сколько раз перемещения, совершённые за второй и третий промежутки времени, больше, чем за первый:

Значит, 0,5 см : 1,5 см : 2,5 см = 1 : 3 : 5. Поскольку эти отношения представляют собой ряд последовательных нечётных чисел, то движение тела было равноускоренным.

В данном случае равноускоренный характер движения был выявлен на основании закономерности (2).

Вопросы

1. По каким формулам рассчитываются проекция и модуль вектора перемещения тела при его равноускоренном движении из состояния покоя?
2. Во сколько раз увеличится модуль вектора перемещения тела при увеличении времени его движения из состояния покоя в n раз?
3. Запишите, как относятся друг к другу модули векторов перемещений тела, движущегося равноускоренно из состояния покоя, при увеличении времени его движения в целое число раз по сравнению с t₁.
4. Запишите, как относятся друг к другу модули векторов перемещений, совершаемых телом за последовательные равные промежутки времени, если это тело движется равноускоренно из состояния покоя.
5. С какой целью молено использовать закономерности (1) и (2)?

Упражнение 8

1. Отходящий от станции поезд в течение первых 20 с движется прямолинейно и равноускоренно. Известно, что за третью секунду от начала движения поезд прошёл 2 м. Определите модуль вектора перемещения, совершённого поездом за первую секунду, и модуль вектора ускорения, с которым он двигался.

2. Автомобиль, двигаясь равноускоренно из состояния покоя, за пятую секунду разгона проходит 6,3 м. Какую скорость развил автомобиль к концу пятой секунды от начала движения?

3. Некоторое тело за первые 0,03 с движения без начальной скорости переместилось на 2 мм, за первые 0,06 с — на 8 мм, за первые 0,09 с — на 18 мм. На основании закономерности (1) докажите, что в течение всех 0,09 с тело двигалось равноускоренно.

Равноускоренное движение

Равноускоренное движение — это движение, при котором вектор ускорения не меняется по модулю и направлению. Примеры такого движения: велосипед, который катится с горки; камень брошенный под углом к горизонту. Равномерное движение — частный случай равноускоренного движения с ускорением, равным нулю.

Рассмотрим случай свободного падения (тело брошено под уголом к горизонту) более подробно. Такое движение можно представить в виде суммы движений относительно вертикальной и горизонтальной осей.

В любой точке траектории на тело действует ускорение свободного падения g→, которое не меняется по величине и всегда направлено в одну сторону. 

Вдоль оси X движение равномерное и прямолинейное, а вдоль оси Y — равноускоренное и прямолинейное. Будем рассматривать проекции векторов скорости и ускорения на оси.

Глупая верность, бездумная храбрость

Победите стражников в Комиссию Тэнре

Переместитесь в Великий храм Наруками и посмотрите новую кат-сцену. Затем бегите за Кудзе Сарой в штаб-квартиру Комиссии Тэнре. Дойдя до нужного места, поговорите с девушкой и войдите в «данж».

Здесь вам предстоит расправиться с большим количеством стражников. Они нападут на вас в 3 волны. Это обычные противники без каких-либо спецатак, поэтому вы запросто расправитесь с ними. Однако в конце придется сразиться с главой отдела внутренних дел клана Кудзе, который представляет собой усиленную версию самурая.

Далее просмотрите новую кат-сцену. На этом задание завершится, а вы получите 650 очков приключений, 31 125 моры, 3 опыта героя и 6 волшебной руды усиления. Не забудьте открыть драгоценный сундук перед уходом из комиссии.

«Охотники за грозами Сэйрая III» (40 камней истока)

Очередной Запирающий камень находится в северной части острова, на вершине горы. Камня нет… Говорим с нашими спутниками и совместно решаем исследовать эту часть острова.

Найдите способ добраться до «Запирающего камня», коснитесь бумажных лент

Прыгаем в «Фазовые ворота» рядом с телепортом и летим куда летится. По сути, использование ворот и есть способ найти Запирающий камень. Терпеливо дожидаемся конца полета, возвращаемся к порталу, откуда начали эту часть задания.

Цель квеста изменилась, теперь это «Коснитесь бумажных лент».

Нажимаем отслеживание и отправляемся ввысь сквозь те же «Фазовые ворота» Все шесты находятся высоко в небе, на летающих обломках, как и сам «Запирающий камень».

Полетом можно немного управлять, поворачивая камеру и задействуя кнопки движения. Полет можно в любой момент прервать, «выпрыгнув» из него и продолжив движение на обычном глайдере (но это нам сейчас не нужно).

Постарайтесь лететь только вверх, поворачивайте камеру «к небу». Доберитесь до громовой сакуры на одном из небесных обломков.

Возьмите электрогранум и летите с ним по «Громовым сферам» (Т). Вы окажетесь на небольшом небесном архипелаге, где есть целых три сакуры. Сориентируйтесь на телепорт и доберитесь до него (там же «Запирающий камень» и один из шестов). Вам будет куда проще добраться до остальных шестов, телепортируясь на этот островок.

Не забудьте: необходимо запомнить количество изгибов на лентах каждого шеста.

Еще два шеста – на других островках вокруг телепорта. Вам просто нужно будет выбрать сакуру, которая стоит с нужной стороны и лететь в сторону метки квеста, после прикосновения к шесту возвращаясь на телепорт.

К одной точке добраться сложно – островки двигаются и могут вас сбросить. Если такое произошло, быстро прыгайте к телепорту и попробуйте еще раз.

Запечатайте «Запирающий камень»

Возвращаемся к камню и выставляем бумажные ленты, как на картинке.

Эта часть задания будет завершена, а небесные камни сложатся в дорогу (чуть выше телепорта), по которой мы направимся к последнему камню.

Видео с лентами и запирающим камнем:

Виды движения и формулы длины пути

Длина пути при равномерном движении (v=const) точки равна:

где t₁ – начало отсчета движения, t₂ – окончание отсчета. Формула (5) показывает то, что длина пути, который проходит равномерно движущаяся материальная точка – это линейная функция времени.

Если движение не является равномерным, то можно длину пути
$\Delta s$ на отрезке времени от
$t$ до
$t + \Delta t$ находят как:

где $\langle v\rangle$ – средняя путевая скорость. При равномерном движении
$\langle v\rangle = v$ .

Путь, который проходит материальная тоска при равнопеременном движении (a=const)вычисляют как:

где a – постоянное ускорение, v – начальная скорость движения.

Глаза Порчи

Найдите место производства и войдите в фабрику

Снова пообщайтесь с Кокоми, но уже в деревне. Она будет стоять неподалеку от вас. Затем телепортируйтесь ко входу в подземелье «Поместье формации», расположенному немного левее шахты Дзякоцу. Спрыгните вниз в сторону отмеченной на мини-карте области.

Оказавшись внизу, отыщите вход в секретный производственный комплекс. Речь идет о небольшом проходе, подсвеченном маркером. Взаимодействуйте с ним для начала сюжетного «данжа».

Отыщите громовые нефриты в фабрике Глаз Порчи

Пройдите вперед и разберитесь с несколькими противниками. Вы также увидите здесь большие двойные двери, для открытия которых требуется отыскать 3 громовых нефрита, расположенных в разных уголках этой локации. Они лежат на небольших алтарях. На скриншотах ниже показано их расположение.

Первый нефрит находится прямо неподалеку от дверей. Затем разломайте ширму и спуститесь на лифте вниз. Разберитесь с противниками и возьмите второй амулет. Теперь поднимитесь по деревянной лесенке и пройдите через небольшую полосу препятствий с электро зарядами.

Далее вам нужно будет прыгать по подъемникам, чтобы взобраться наверх и найти там последний громовой нефрит. Заполучив все «ключи», спрыгните вниз и идите к заблокированным дверям. Откройте их, пройдите внутрь и разберитесь со всеми застрельщиками фатуи. Первым делом советуем расправиться с Гидро врагом, так как он лечит своих союзников.

Далее вам нужно будет расправиться с Начальником фабрики Наташкой, представляющей собой усиленную версию зеркальной девы. Неприятный враг, однако победить его сравнительно несложно при наличии в команде хорошего щитовика, например, Чжун Ли, а также Пиро и Крио героев.

Победив мини-босса, вы столкнетесь со Скарамуччей, предвестником Фатуи. Драться с ним не придется, поэтому просто посмотрите кат-сцену, в рамках которой вы окажитесь в Великом храме Наруками и поговорите с Яэ Мико. На этом задание завершится. Вы получите в награду 450 очков приключений, 30 камней истока, 22 000 моры, 2 опыта героя и 4 волшебной руды усиления.

Дворцовая дуэль

Направляйтесь в резиденцию Тэнсюкаку

Вам нужно догнать Сару, которая отправилась в резиденцию, показанную на карте квестовым маркером. Просто доберитесь до указанного места, а затем начните подземелье «Остров Наруками: Тэнсюкаку». Пройдите вперед и поболтайте с Синьорой. Далее вас ждет битва с боссом.

Как победить Синьору

В этой битве босс будет в ослабленном состоянии, поэтому сразить его будет легче, чем в рамках еженедельных испытаний. Однако он все равно может создать вам немало проблем. Крайне рекомендуем иметь в команде персонажа, способного накладывать щиты (например, Чжун Ли или Диону), так как от некоторых атак Синьоры крайне трудно уклониться.

Во время битвы предвестник Фатуи будет использовать две формы: Крио и Пиро, нанося соответствующий урон и имея высокое сопротивление к ледяным или огненным атакам. Поэтому следует избегать применения этих стихий в указанные моменты времени, чтобы нанести боссу максимальный урон.

Необходимо также следить за полоской температуры, расположенной наверху шкалы здоровья. Если она полностью заполнится, то вы начнете получать повреждения. Чтобы согреться или, наоборот, охладиться нужно подойти к специальным механизмам, стоящим по углам помещения, и уничтожить их. Перед этим, скорее всего, нужно будет взять мотыльков лотоса.

Когда у Синьоры останется мало здоровья, она закроет себя кристаллом, который можно разрушить только с помощью элементальных реакций. После того как уничтожите его, босс перейдет в следующую форму – Тлеющая алая ведьма. Именно здесь она начнет применять огненные атаки.

Разобравшись с противником, посмотрите новую кат-сцену. В ней Райдэн казнит Синьору. На этом задание завершится, а вы получите в награду 925 очков приключений, 30 камней истока, 44 000 моры, 4 опыта героя и 8 волшебной руды усиления.

«Охотники за грозами Сэйрая IV» (40 камней истока, роскошный и драгоценный сундуки)

Остался последний «Запирающий камень». Неужели нам удастся остановить чудовищную грозу на этом острове?

Берем электрогранум на краешке островка с телепортом (на метке, куда нас отправляет квест) и летим в направлении следующей метки.

Подбираем по пути электрогранумы, летим дальше, и ни в коем случае не сходим с «небесной» дороги. Последний «Запирающий камень» тоже на обломках в небе, прямо около очередного телепорта.

Вблизи метки придется пройтись по дорожке из сдвигающихся камней, не забудьте взять перед ними электрогранум – когда эта дорожка кончится, придется лететь.

Добираемся до телепорта. «Запирающий камень» и все три шеста стоят в одном месте.

Коснитесь бумажных лент, запечатайте «Запирающий камень»

Тут все очень просто, как и с первым камнем – все рядом и наглядно. В центре острова, где бушевала грозовая буря, возникнет каменная платформа.

Продолжить исследование, победить врагов

Убедитесь, что вы надели «Сухпаек №30». Отправляемся на эту платформу, слетев туда прямо от телепорта. Летим в кромешной тьме, но зато уже без беспрестанно бьющих куда попало (в том числе и в наших персонажей) молний.

В полете задача меняется: «Победите врагов».

Знакомимся с «Манифестацией грома», океанидом с электроуклоном.

Здесь не нужно убивать призываемых существ. Необходимо уворачиваться от атак, вовремя кушать и лупить самого босса.

У него множество неприятных умений, вроде сдвигающихся электрических стен (сквозь них можно выбегать, пока они не сдвинулись), вертушки (удирать), движущаяся клетка молний (драпать!!!), электрошипов, круговых зон на земле (выбегать) и прочей нехорошей гадости.

«Продолжайте исследование»

Отправляемся на метку квеста, берем электрогранум и летим (Т) вверх, потом еще выше.

Находим драгоценный и роскошный сундуки ( в них пара чертежей декора), 1 электрокул и какие-то странные перья. Паймон предлагает показать их нашим соратникам, Тайсуке и Эйко, может, они что-то знают.

Находим метку квеста на карте и телепортируемся к искателям приключений.

Поговорив с ними, оставляем «Странное перо» себе (что с ним делать, мы пока не знаем, но скорее всего, перо понадобится в одном из следующих квестов), получаем награду и достижение «Охотники за грозами Сэйрая» и любуемся островом, который теперь можем почти безопасно исследовать.

Самый центр аномалии, пик Амакумо, все еще остается опасным местом, подверженным Громовому бедствию.

Определение и формула пути

Линия, которую описывает материальная точка при своем движении, называется траекторией.

Определение

Длиной пути называют сумму длин всех участков траектории, которые прошла точка за рассматриваемый промежуток времени
от t₁ до t₂.

В том случае, если уравнения движения представлены в прямоугольной декартовой системе координат, то длина пути (s) определяется как:

В цилиндрических координатах длина пути может быть выражена как:

В сферических координатах формулу длины пути запишем:

Местоположение перемещающейся материальной точки в фиксированный момент времени, например t=t₁ называют начальным положением.
Очень часто полагают t₁=0. Длин пути, который прошла материальная точка из начального положения – скалярная функция времени: s=s(t).

Считают, что за промежуток времени $d t \rightarrow 0$ материальная точка проходит путь ds,
который называют элементарным. При этом:

где $\bar{r}$ – вектор элементарного перемещения материальной точки, v – модуль скорости ее движения.

Закон равноускоренного движения

Закон равноускоренного движения

y=y+vt+at22.

Еще одна распространенная задача кинематики, которая возникает при анализе равноускоренного движения — нахождение координаты при заданных значениях начальной и конечной скоростей и ускорения.

Исключая из записанных выше уравнений t и решая их, получаем:

s=v2-v22a.

По известным начальной скорости, ускорению и перемещению можно найти конечную скорость тела:

v=v2+2as.

При v= s=v22a и v=2as

Важно!

Величины v, v, a, y, s, входящие в выражения, являются алгебраическими величинами. В зависимости от характера движения и направления координатных осей в условиях конкретной задачи они могут принимать как положительные, так и отрицательные значения.

Всё ещё сложно?
Наши эксперты помогут разобраться

Все услуги

Решение задач

от 1 дня / от 150 р.

Курсовая работа

от 5 дней / от 1800 р.

Реферат

от 1 дня / от 700 р.

Задачи на Свободное падение с решениями

Формулы, используемые в 9 классе на уроках
«Задачи на Свободное падение тел».

Название величины	Обозначение	Единица измерения	Формула
Время		с
Проекция начальной скорости		м/с
Проекция мгновенной скорости		м/с
Проекция ускорения		м/с2
Проекция перемещения		м
Координата		м

ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ

Задача № 1.
 С балкона 8-го этажа здания вертикально вниз бросили тело, которое упало на землю через 2 с и при падении имело скорость 25 м/с. Какова была начальная скорость тела?

Задача № 2.
 Какой высоты достигнет мяч, брошенный вертикально вверх со скоростью 20 м/с? Сколько времени для этого ему понадобится?

Задача № 3.
 Мяч бросили вертикально вверх со скоростью 15 м/с. Через какое время он будет находиться на высоте 10 м?

Задача № 4.
 Через сколько секунд мяч будет на высоте 25 м, если его бросить вертикально вверх с начальной скоростью 30 м/с?Ответ: через 1 с и через 5 с.

Задача № 5.
 Лифт начинает подниматься с ускорением а = 2,2 м/с2. Когда его скорость достигла v = 2,4 м/с, с потолка кабины лифта оторвался болт. Чему равны время t падения болта и перемещение болта относительно Земли за это время? Высота кабины лифта Н = 2,5 м.

Ответ: 0,645 с; болт перемещается относительно Земли на 0,49 м вниз.

Задача № 6. (повышенной сложности)
 Одно тело свободно падает с высоты h₁; одновременно с ним другое тело начинает движение с большей высоты h₂. Какой должна быть начальная скорость v второго тела, чтобы оба тела упали одновременно?

Задача № 7. (олимпиадного уровня)
 Из окна, расположенного на высоте 30 м, начинает падать без начальной скорости тяжелый цветочный горшок. В этот момент точно под окном проезжает велосипедист. При какой скорости движения велосипедиста расстояние между ним и горшком будет все время увеличиваться?

Ответ: v > 17 м/с.

Задача № 8.
   ЕГЭ
 С воздушного шара, поднимающегося со скоростью v = 1 м/с, падает камень и достигает земли спустя t = 16 с. На какой высоте h находился шар в момент сбрасывания камня? С какой скоростью v камень упал на землю?

Задача № 9.
 На какой высоте скорость тела, брошенного вертикально вверх с начальной скоростью v, уменьшится в 4 раза?

Дано: Vo, V = Vo/4.
Найти: h — ?Решение:

Если принять, что g ≈ 10 м/с2 , то h = 15 • Vo^2 / 320 ≈ 0,047 • Vo^2.

Ответ: h = (15 • Vo^2) / (32 • g) ≈ 0,047 • Vo^2.

Краткое пояснение для решения ЗАДАЧИ на Свободное падение тел.

Свободное падение — это движение тела под действием силы тяжести (другие силы — сила сопротивления, выталкивающая сила — отсутствуют либо ими пренебрегают).

Так как сила тяжести направлена вниз, то ускорение, которое она сообщает телу, тоже направлено вниз. Свободное падение — это равноускоренное движение. Ускорение, сообщаемое телу силой тяжести, называют ускорением свободного падения. Оно одинаково для всех тел вблизи поверхности Земли и имеет значение 9,8 м/с2. При решении задач в большинстве случаев это число округляется до 10 м/с2.

При решении задач применяются формулы равноускоренного движения. Для нахождения проекций векторов координатную ось обычно обозначают буквой у, так как движение происходит по вертикали. Направляют ее вверх или вниз — как удобней при решении конкретной задачи. Скорость свободно падающего тела возрастает.

Движение тела, брошенного вертикально вверх — частный случай свободного падения. Только скорость тела уменьшается, так как оно движется против силы тяжести, и вектор начальной скорости и вектор ускорения противоположно направлены. Достигая некоторой точки (наивысшей точки подъема), тело на мгновение останавливается (в это время его скорость равна нулю), а затем начинает падать. Так как движение вверх и вниз происходит с одинаковым ускорением, то время подъема и время падения тела равны.

Если координатную ось направить вверх, то проекция ускорения будет отрицательна, если вниз — положительна. Но при любом направлении оси для падающего тела векторы ускорения и скорости сонаправлены, а для тела, брошенного вверх — противоположно направлены.

Это конспект по теме «ЗАДАЧИ на Свободное падение тел с решениями». Выберите дальнейшие действия:

• Перейти к теме: ЗАДАЧИ на применение Законов Ньютона
• Посмотреть конспект по теме КИНЕМАТИКА: вся теория для ОГЭ (шпаргалка)
• Вернуться к списку конспектов по Физике.
• Проверить свои знания по Физике.

1.6. Контроль расхода боеприпасов

Одной из обязанностей командира по обеспечению организованного и действенного огня в бою является контроль за расходом боеприпасов. Командир должен постоянно следить за наличием боеприпасов в подразделении и принимать меры к их пополнению.

Запас патронов автоматчики (пулеметчики) носят в магазинах и обоймах, уложенных в сумки.

Обеспечение патронами автоматчиков (пулеметчиков) в бою производится подносчиками патронов, выделенными командиром подразделения.

По израсходовании половины носимого запаса автоматчик (пулеметчик) докладывает об этом своему командиру.

Один магазин к автомату и три магазина к пулемету, снаряженных патронами, должны быть всегда у автоматчика (пулеметчика) как неприкосновенный запас, который расходуется только с разрешения командира.